Made of special high-density reaction-bonded silicon carbide, the SEU Starbar is a tube element with both electrical connections on one end. The hot zone is formed by cutting a slot, which reduces the cross sectional area over which the current flows, resulting in higher resistance than the cold end. The cold end is formed by cutting two longitudinal slots along the length of the tube and is made of LRE (low resistance end) material and in most cases is larger in diameter.
The SEU element is supplied with a ceramic collar cemented to the cold end. The cold end of the SEU element is flame sprayed with aluminum for a distance of about two inches. Flat, braided-aluminum straps are held in compression with a stainless steel clamp to this metallized area. The clamp is electrically insulated from the flat braid with high temperature insulation. The aluminum element braid is ten inches long and holes are provided for easy connection to the power supply.
The electrical resistance of the SEU can be customized by varying the spiral width. SEU Starbars can range from high resistance to low resistance. The electrical resistance can be as high as the SER (spiral element with return) and as low as the RR (rammed type) non-spiral Starbar. There are further limits based on the size of the SEU.
SEU Starbars are described by giving the overall length, the heating section length, and the diameter. As an example, SEU 45 x 30 x 1-1/4 is a SEU Starbar, 45" overall length, 30" hot zone, and 1-1/4" hot zone outer diameter. In metric, SEU 1143 x 762 x 32 is a SEU Starbar, 1143 mm overall length, 762 mm hot zone and 32 mm hot zone outer diameter.
SEU Brochure
(PDF, 1138KB)
Sizing Breakdown
| Item # | Hot Zone Nominal Diameter | Cold End Diameter | Collar Diameter | Collar Location | Strap Rating |
|---|---|---|---|---|---|
| SEU-1/2-13 | 1/2 inch 13 mm | 7/8 Inch 22 mm | 1-9/16 Inch 40 mm | 2 Inch 50 mm | 50 Amp |
| SEU-5/8-16 | 5/8 Inch 16 mm | 1 Inch 25 mm | 2-3/8 Inch 60 mm | 2 Inch 50 mm | 50 Amp |
| SEU-3/4-19 | 3/4 Inch 19 mm | 1-3/8 Inch 35 mm | 2-3/8 Inch 60 mm | 2 Inch 50 mm | 100 Amp |
| SEU-1-25 | 1 Inch 25 mm | 1-1/2 Inch 38 mm | 2-3/8 Inch 60 mm | 3 Inch 4 76 mm | 100 Amp |
| SEU-1-1/4-32 | 1-1/4 Inch 32 mm | 2-1/8 Inch 54 mm | 3-5/32 Inch 80 mm | 3 Inch 76 mm | 100 Amp |
| SEU-1-1/2-38 | 1-1/2 Inch 38 mm | 2-3/8 Inch 60 mm | 3-15/16 Inch 100 mm | 3 Inch 76 mm | 100 Amp |
| SEU-1-3/4-44 | 1-3/4 Inch 44 mm | 2-3/4 Inch 70 mm | 3-15/16 Inch 100 mm | 3 Inch 76 mm | 200 Amp |
| SEU-2-1/8-54 | 2-1/8 Inch 54 mm | 2-3/4 Inch 70 mm | 3-15/16 Inch 100 mm | 3 Inch 76 mm | 200 Amp |
| SEU-2-3/4-70 | 2-3/4 Inch 70 mm | 2-3/4 Inch 70 mm | 3-15/16 Inch 100 mm | 4 Inch 95 mm | 400 Amp |
Specifications
Operating Temperatures
In clean dry air, SEU Starbars can be operated at furnace control temperatures up to 2912°F (1600°C).
In inert atmospheres of argon or helium, SEU elements may be operated to 3092°F (1700°C).
In reducing atmospheres the maximum operating temperature is 2500°F (1370°C).
There is a protective coating of silicon dioxide on the silicon carbide. Hydrogen reduces this coating and causes the Starbar to deteriorate. Very dry or very wet hydrogen is detrimental to long service life.
Nitrogen atmosphere applications are limited to 2500°F (1370°C) and 30 watts per square inch (5 watts per square centimeter) maximum surface watt loading. Too high of a surface temperature will result in a silicon nitride reaction. A thermally insulative layer forms around the Starbar resulting in very high surface temperatures which damage the Starbars.
Engineering Information
Superior Performance
At 2.85 gms/cc, this high-density low-porosity element is able to survive severe environments. The high density prevents the internal structure from being oxidized or corroded. This element therefore has an extremely slow aging characteristic.
Electrical Characteristics
The SEU STARBAR has a negative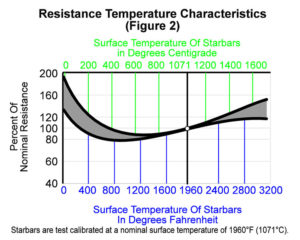
Electrical Loading
Starbars are not sized to a specific wattage output like metallic heating elements. The amount of energy that a Starbar is capable of converting from electrical to heat energy depends on the ambient furnace temperature and atmosphere in which the Starbar is operating.
When calculating the wattage capabilities of a Starbar, the unit of watts output per unit of radiating surface area is used. Follow the recommended watt loading for a square inch or square centimeter of radiating surface as a function of furnace temperature.
To determine the recommended wattage capabilities of the Starbars, start with the “Recommended Maximum Watt Loading” chart. Knowing the furnace temperature and atmosphere in which the Starbars will be operated, follow the temperature line until you intersect the heavy black line (choosing the appropriate line according to the atmosphere in which the Starbar will be operating). Read the loading in watts per square unit of radiating surface that can be applied to the Starbar. To find the total amount of power one Starbar could supply under these conditions, multiply this value by the radiating surface area of the Starbar. The radiating surface area is calculated by multiplying the diameter by the hot zone length by pi (3.142).
Example: At 2750ºF, in air, a Starbar could be loaded to 35 watts per square inch. Therefore, a Starbar with 10 square inches of radiating surface could supply 350 watts, whereas a Starbar with 200 square inches of radiating surface could supply 7000 watts.
Metric Calculation: At 1500ºC, in air, the Starbar could be loaded to 6 watts per square centimeter. Therefore, a Starbar with 100 square centimeters of radiating surface could supply 600 watts, whereas a Starbar with 2000 square centimeters of radiating surface could supply 12,000 watts.
Example of radiating area:
The SEU 45 x 30 x 1-1/4 has a hot zone length of 30 inches and a diameter of 1.25 inch. The radiating surface area is 30 x 1.25 x 3.14, or 118 square inches.
Metric Calculation: The SEU 1143 x 762 x 32mm has a hot zone length of 762mm and a diameter of 32mm. The radiating surface area is 762 x 32 x 3.14 or 76,566 square millimeters — converted to centimeters is 766 square centimeters.

Power Supply
The previous paragraph explained how to calculate the recommended wattage output of the Starbar. The following explains how to compute the electrical requirements to provide the recommended power.
Knowing the wattage output and the resistance of the Starbar you have two parts of an equation with three unknowns. This equation is E=√ (W x R), (E = nominal full load voltage, W = rating of the Starbar in watts, R = resistance of the Starbar in ohms). The resistance of the Starbar can be calculated using the values found in Table B.
Solving for E determines the voltage required on a nominal-resistance Starbar to provide the wattage output desired. This assumes a nominal resistance.
Example: A Starbar SEU 24 x 16 x 1.25 has a resistance of 5.76 ohms and 63 square inches of radiating surface. Loading to 40 watts per square inch this Starbar could provide 2500 watts. To find the nominal voltage, solve for E.
- E = √(W x R)
- E = √(2500 x 5.76
- E = 120 volts
Starbars may be connected in parallel, series, or combination thereof. Parallel connections are preferred because if the resistance of one or more Starbars increases, its portion of the load will be reduced and the group will remain in balance.
In a parallel arrangement the voltage across all the Starbars is the same. In the formula W = E2÷R (W = watts, E = voltage, R = resistance) it can be seen that the greater the resistance, the lower the wattage output. The Starbars in the parallel circuit with the lowest resistance will supply more heat energy and therefore operate at a higher temperature.
This higher Starbar temperature will cause it to gradually increase in resistance until all the Starbars have the same resistance. At this time all the Starbars should have approximately the same resistance values and surface temperatures and therefore remain in balance.
To compute the network resistance of a group of Starbars the following formula may be used: Rn = R x S ÷ P (Rn = network resistance, R = resistance of Starbar, S = number of Starbars connected in a series, P = number of parallel circuits).
Example: Eight Starbars SEU 24 x 16 x 1.25 (R = 5.76 ohms) connected 2 in series (S = 2) and 4 parallel groups (P = 4).
- Rn = R x S ÷ P
- Rn = 5.76 x 2 ÷ 4
- Rn = 2.88 ohms
To compute the nominal network voltage required to power a set of Starbars, a combination of the previous two formulas is used as follows:
En = √(Wt x Rn), (En = nominal network voltage, Rn = network resistance, Wt = total wattage output).
Example: Eight Starbars SEU 24 x 16 x 1.25 (R = 5.76 ohms) connected 2 in series, 4 parallel groups. Each Starbar provides 2500 watts. Wt = 8 x 2500 = 20,000 watts. Rn = 2.88 ohms.
- En = √(Wt x Rn)
- En = √(20,000 x 2.88)
- En = 240 volts
The resistance of Starbars increases gradually during their useful life. Therefore some means of keeping the power input to the kiln or furnace at a level sufficiently high to maintain the desired temperature is required.
Historically, expensive voltage varying equipment such as multiple tap transformers or saturable reactors were recommended for all but the very low temperature applications.
SEU Starbars can be used directly on the line (fixed voltages) at temperatures up to 2500ºF (1370ºC). To compensate for the reduced output as the Starbars gradually age or increase in resistance, the furnace or kiln is initially overpowered by 25% to 50%.
This type of arrangement eliminates the expensive voltage varying equipment and has proven very satisfactory in many applications. Fixed voltage supply is not recommended when fine process temperature control is required.
Assume a furnace will require approximately 20,000 watts after all heat losses and load factors have been considered. Increasing this 20,000 by 25% to 50% gives a wattage requirement of between 25,000 and 30,000 watts.
By taking another look at the previous examples it can be seen that 10 Starbars SEU 24 x 16 x 1.25 connected two in series, five parallel groups on 240 volts would supply 25,000 watts. If 12 Starbars of the same size Starbars were used, the output would be 30,000 watts.
Twelve Starbars connected four in series, per phase, on 240 volts would make a balanced three phase 240 volt network.
The temperature of the kiln or furnace is controlled by an off-on controller. When the Starbars are new, they will only be powered for 20/25 or 20/30 of the time (the ratio of the power needed to the power available). As the Starbars increase in resistance, they will be on for a greater percentage of the time. When they have increased in resistance to a point at which they supply 30,000 watts, they will be on 100% of the time. A SCR (silicon controlled rectifier) or thyrister can also be used.
For applications where close temperature control is desired and/or for temperatures above 2500ºF (1370ºC), a device for increasing the voltage to the Starbars is required. There are several methods of providing this variable voltage source.
- Multiple tap transformers are the most common because it is usually the least expensive. The secondary of the transformer is provided with taps that usually vary in number from 10 to 36. By carefully selecting the voltage taps, the correct voltage output to match the resistance of the Starbars over their complete useful life can be made.
- Saturable reactors and induction regulators are used to provide a stepless voltage control. They are also sometimes used with multiple tap transformers.
- Capacitor controls are used infrequently. They, of course, will tend to improve a power factor that makes their use desirable in some areas.
- Silicon controlled rectifiers (SCR) have become quite popular with the advances in solid state devices.
To compensate for the reduced output as the Starbars increase in resistance, a voltage range is required that will compensate for a 100% increase in the Starbar resistance. The following formula may be used to figure Emax: Emax = √ (Wt x Rn) x 1.5, (Emax = recommended maximum voltage required to compensate for increase in resistance due to aging and resistance tolerance, Wt = rating of transformer in watts, Rn = network resistance of the Starbars, 1.5 = minimum margin to accommodate the doubling of the Starbar network resistance and the plus 20% resistance tolerance). A higher value will offer slightly longer usable service life.
Example: A transformer is rated at 24 KVA and has a computed nominal full load voltage of 240 volts. (Rn = 2.88, Wt = 20,000 for 8 Starbars)
- Emax = √(Wt x Rn) x 1.5
- Emax = √(20,000 x 2.88) x 1.5
- Emax = √(57,600) x 1.5
- Emax = 360 volts
The nominal full load voltage and maximum voltage have been computed.
When specifying the transformer, the nominal full load voltage is usually reduced to allow for the minus 20% resistance tolerance of the Starbars and slow furnace heatup.
To calculate the minimum voltage, take 70% of the nominal voltage. For periodic applications, take 30% of the nominal full load voltage.
Auto transformers may be used if primary voltage is 230 volts or less. They should not be used in a three phase arrangement. Accepted practice limits the secondary voltage on all transformers to 300 volts. Above this, refractory voltage leakage becomes a problem.
When computing the size of the voltage steps between taps, a value of 5% of the nominal full load voltage is often used. When SCR or thyrister controls are used on the primary, fewer taps are required. For example, if 6 taps are used, the idling tap can be 0.7 x nominal voltage, then each consecutive tap would be 14% higher. For 8 taps, the idling tap would again be 0.7 x nominal voltage, each consecutive tap at 9.1% higher than the preceding.
Custom Electrical Resistance
Ease of Replacement
SEU Starbars can be replaced while the furnace is at operating temperature. The power to the Starbars being changed should be shut off. The aluminum braids can then be disconnected from the buss and the old elements removed. The new Starbar should be inserted smoothly through the hot furnace with sufficient speed to insure that the aluminum is not melted off the terminal end but not so fast as to cause thermal shock.
Element Spacing
Service Life
Starbars increase gradually in resistance with use. This characteristic of increasing in resistance is called aging. Aging is a function of the following:
- Operating temperature
- Electrical loading – usually expressed in watts per square inch or watts per square centimeter of Starbar radiating surface
- Atmosphere
- Type of operation (continuous or intermittent)
- Operating and maintenance techniques
Mounting
The terminal holes should be 10% larger than the diameter of the element. Extreme caution should be used when mounting to ensure that the Starbars are not placed in tension. There should be adequate freedom to allow the furnace and Starbars to expand and contract independently.
Starbars should have their heating sections centered in the furnace chamber so that no portion of the heating section extends into the furnace wall. A conical or truncated cone shaped recess 1/2 inch (13 mm) deep is sometimes located on the interior wall where the Starbar passes through. This allows the hot zone to radiate properly and helps maintain a uniform temperature in the kiln.
Furnace Heating Chamber
Recommended Starbar Spacing
X = 2 x Starbar hot zone diameter is the minimum, 1.5 x Starbar hot zone diameter is the absolute minimum and requires a reduced Starbar surface watt loading
Z = S ÷ 1.73 minimum for moving loads
S = 2 x Starbar hot zone diameter minimum
X – distance from the centerline of Starbar to any reflecting surface, such as a refractory wall or product
Z – distance from the centerline of the Starbar to a moving or stationary load
S – distance from centerline of one Starbar to the centerline of an adjacent Starbar
Specifications and Matching
SEU in protection tube
Availability
Notes
The end clip hole diameter for 50 amp braid is 9/32″ (7 mm), 100 amp braid and over is 9/16″ (14 mm).
The resistance of the SEU Starbar is dependent on the spiral. The more spiral turns, the higher the resistance.
All Resistance values are +/- 20%.



